Draw a Circle Using Integer Arithmetic Only

Rasterizing a circumvolve of radius 23 with the Bresenham midpoint circle algorithm. Only the green octant is actually calculated, information technology'southward only mirrored eight times to form the other seven octants.

A circle of radius 23 drawn by the Bresenham algorithm

In computer graphics, the midpoint circle algorithm is an algorithm used to determine the points needed for rasterizing a circumvolve. Bresenham'south circle algorithm is derived from the midpoint circle algorithm.^{[ citation needed ]} The algorithm can be generalized to conic sections.^[one]

The algorithm is related to work by Pitteway^[two] and Van Aken.^[iii]

Summary [edit]

This algorithm draws all viii octants simultaneously, starting from each cardinal direction (0°, 90°, 180°, 270°) and extends both means to accomplish the nearest multiple of 45° (45°, 135°, 225°, 315°). Information technology can determine where to stop because when y = x, information technology has reached 45°. The reason for using these angles is shown in the higher up flick: As x increases, it does not skip nor repeat any x value until reaching 45°. And then during the while loop, 10 increments by i each iteration, and y decrements by one on occasion, never exceeding one in one iteration. This changes at 45° because that is the bespeak where the tangent is rise=run. Whereas rise>run earlier and rise<run after.

The second part of the problem, the determinant, is far trickier. This determines when to decrement y. It usually comes afterwards cartoon the pixels in each iteration, considering it never goes below the radius on the first pixel. Considering in a continuous part, the function for a sphere is the part for a circle with the radius dependent on z (or whatever the 3rd variable is), information technology stands to reason that the algorithm for a discrete(voxel) sphere would as well rely on this Midpoint circle algorithm. But when looking at a sphere, the integer radius of some side by side circles is the same, but it is non expected to have the same exact circumvolve next to itself in the aforementioned hemisphere. Instead, a circle of the aforementioned radius needs a different determinant, to let the bend to come in slightly closer to the center or extend out farther.

• One hundred fifty concentric circles fatigued with the midpoint circle algorithm.

• 

  On left, all circles are drawn blackness.

• 

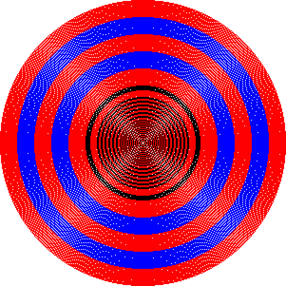
  On right, red, black and blueish are used together to demonstrate the concentricity of the circles.

Algorithm [edit]

The objective of the algorithm is to approximate the curve ${\displaystyle x^{2}+y^{2}=r^{2}}$ using pixels; in layman's terms every pixel should be approximately the same altitude from the center. At each step, the path is extended by choosing the adjacent pixel which satisfies ${\displaystyle ten^{two}+y^{2}\leq r^{2}}$ but maximizes ${\displaystyle x^{ii}+y^{2}}$ . Since the candidate pixels are side by side, the arithmetic to calculate the latter expression is simplified, requiring merely bit shifts and additions. But a simplification tin be done in guild to sympathize the bitshift. Keep in listen that a left bitshift of a binary number is the aforementioned as multiplying with 2. Ergo, a left bitshift of the radius only produces the diameter which is defined as radius times two.

This algorithm starts with the circumvolve equation. For simplicity, assume the center of the circumvolve is at ${\displaystyle (0,0)}$ . Consider offset the first octant just, and draw a curve which starts at point ${\displaystyle (r,0)}$ and proceeds counterclockwise, reaching the angle of 45.

The fast direction here (the basis vector with the greater increment in value) is the ${\displaystyle y}$ direction. The algorithm always takes a pace in the positive ${\displaystyle y}$ direction (up), and occasionally takes a pace in the ho-hum direction (the negative ${\displaystyle x}$ management).

From the circumvolve equation is obtained the transformed equation ${\displaystyle x^{two}+y^{ii}-r^{2}=0}$ , where ${\displaystyle r^{two}}$ is computed only one time during initialization.

Permit the points on the circle be a sequence of coordinates of the vector to the point (in the usual basis). Points are numbered according to the order in which drawn, with ${\displaystyle north=ane}$ assigned to the first point ${\displaystyle (r,0)}$ .

For each signal, the following holds:

${\displaystyle {\begin{aligned}x_{n}^{two}+y_{n}^{2}=r^{ii}\end{aligned}}}$

This can be rearranged thus:

${\displaystyle {\begin{aligned}x_{n}^{ii}=r^{two}-y_{northward}^{2}\end{aligned}}}$

And likewise for the next point:

${\displaystyle {\brainstorm{aligned}x_{n+1}^{2}=r^{2}-y_{n+1}^{two}\terminate{aligned}}}$

Since for the first octant the next point will always exist at least one pixel college than the concluding (but also at most 1 pixel higher to maintain continuity), information technology is truthful that:

${\displaystyle {\begin{aligned}y_{n+1}^{2}&=(y_{due north}+1)^{2}\\&=y_{n}^{two}+2y_{north}+1\stop{aligned}}}$

${\displaystyle {\begin{aligned}x_{n+one}^{2}=r^{2}-y_{due north}^{two}-2y_{n}-ane\terminate{aligned}}}$

And so, rework the side by side-indicate-equation into a recursive ane by substituting ${\displaystyle x_{n}^{two}=r^{ii}-y_{n}^{2}}$ :

${\displaystyle {\begin{aligned}x_{n+i}^{ii}=x_{due north}^{two}-2y_{north}-1\stop{aligned}}}$

Considering of the continuity of a circle and because the maxima along both axes is the same, clearly it will non be skipping x points as information technology advances in the sequence. Usually it stays on the aforementioned ten coordinate, and sometimes advances by ane.

The resulting coordinate is then translated by adding midpoint coordinates. These frequent integer additions exercise not limit the performance much, as those foursquare (root) computations tin be spared in the inner loop in plough. Again, the naught in the transformed circle equation is replaced by the error term.

The initialization of the fault term is derived from an offset of ½ pixel at the get-go. Until the intersection with the perpendicular line, this leads to an accumulated value of ${\displaystyle r}$ in the fault term, so that this value is used for initialization.

The frequent computations of squares in the circumvolve equation, trigonometric expressions and square roots can again be avoided by dissolving everything into single steps and using recursive ciphering of the quadratic terms from the preceding iterations.

Variant with integer-based arithmetic [edit]

Merely as with Bresenham'southward line algorithm, this algorithm can exist optimized for integer-based math. Because of symmetry, if an algorithm tin can be found that only computes the pixels for 1 octant, the pixels can be reflected to get the whole circumvolve.

Nosotros kickoff by defining the radius error as the difference between the exact representation of the circle and the center point of each pixel (or any other arbitrary mathematical signal on the pixel, so long as it's consequent across all pixels). For whatever pixel with a heart at ${\displaystyle (x_{i},y_{i})}$ , the radius fault is defined equally:

${\displaystyle RE(x_{i},y_{i})=\left\vert x_{i}^{2}+y_{i}^{2}-r^{2}\correct\vert }$

For clarity, this formula for a circumvolve is derived at the origin, but the algorithm can be modified for any location. It is useful to start with the point ${\displaystyle (r,0)}$ on the positive X-axis. Because the radius volition be a whole number of pixels, conspicuously the radius error will be zero:

${\displaystyle RE(x_{i},y_{i})=\left\vert x_{i}^{2}+0^{2}-r^{two}\right\vert =0}$

Because it starts in the first counter-clockwise positive octant, it will pace in the direction with the greatest travel, the Y direction, then it is clear that ${\displaystyle y_{i+1}=y_{i}+1}$ . Also, because information technology concerns this octant only, the X values have only 2 options: to stay the same as the prior iteration, or decrease by 1. A conclusion variable can exist created that determines if the following is true:

${\displaystyle RE(x_{i}-1,y_{i}+one)<RE(x_{i},y_{i}+1)}$

If this inequality holds, then plot ${\displaystyle (x_{i}-1,y_{i}+1)}$ ; if non, then plot ${\displaystyle (x_{i},y_{i}+1)}$ . So, how to determine if this inequality holds? Starting time with a definition of radius error:

${\displaystyle {\brainstorm{aligned}RE(x_{i}-1,y_{i}+i)&<RE(x_{i},y_{i}+1)\\\left\vert (x_{i}-1)^{2}+(y_{i}+1)^{two}-r^{two}\correct\vert &<\left\vert x_{i}^{two}+(y_{i}+1)^{two}-r^{two}\right\vert \\\left\vert (x_{i}^{2}-2x_{i}+1)+(y_{i}^{2}+2y_{i}+1)-r^{2}\right\vert &<\left\vert x_{i}^{2}+(y_{i}^{two}+2y_{i}+1)-r^{2}\right\vert \\\cease{aligned}}}$

The absolute value function does not help, and then square both sides, since a square is always positive:

${\displaystyle {\brainstorm{aligned}\left[(x_{i}^{ii}-2x_{i}+i)+(y_{i}^{2}+2y_{i}+one)-r^{2}\correct]^{2}&<\left[x_{i}^{two}+(y_{i}^{2}+2y_{i}+1)-r^{2}\right]^{2}\\\left[(x_{i}^{ii}+y_{i}^{ii}-r^{2}+2y_{i}+ane)+(1-2x_{i})\right]^{two}&<\left[x_{i}^{2}+y_{i}^{2}-r^{2}+2y_{i}+one\right]^{2}\\\left(x_{i}^{two}+y_{i}^{2}-r^{ii}+2y_{i}+1\right)^{2}+2(1-2x_{i})(x_{i}^{2}+y_{i}^{2}-r^{2}+2y_{i}+ane)+(ane-2x_{i})^{2}&<\left[x_{i}^{ii}+y_{i}^{ii}-r^{2}+2y_{i}+ane\right]^{two}\\2(1-2x_{i})(x_{i}^{two}+y_{i}^{ii}-r^{two}+2y_{i}+1)+(one-2x_{i})^{2}&<0\\\end{aligned}}}$

Since x > 0, the term ${\displaystyle (1-2x_{i})<0}$ , so dividing gets:

${\displaystyle {\begin{aligned}2\left[(x_{i}^{2}+y_{i}^{2}-r^{ii})+(2y_{i}+1)\right]+(1-2x_{i})&>0\\2\left[RE(x_{i},y_{i})+Y_{\text{Change}}\right]+X_{\text{Change}}&>0\\\end{aligned}}}$

Thus, the determination criterion changes from using floating-point operations to unproblematic integer addition, subtraction, and bit shifting (for the multiply past two operations). If ${\displaystyle 2(RE+Y_{\text{Change}})+X_{\text{Change}}>0}$ , then decrement the X value. If ${\displaystyle ii(RE+Y_{\text{Change}})+X_{\text{Alter}}\leq 0}$ , so keep the same X value. Again, by reflecting these points in all the octants, a full circle results.

We may reduce ciphering by only calculating the delta between the values of this determination formula from its value at the previous step. Nosotros start by assigning ${\displaystyle E}$ as ${\displaystyle iii-2r}$ which is the initial value of the formula at ${\displaystyle (x_{0},y_{0})=(r,0)}$ , then as above at each stride if ${\displaystyle Eastward>0}$ we update it every bit ${\displaystyle E=Due east+2(v-2x+2y)}$ (and decrement 10), otherwise ${\displaystyle E=E+ii(3+2y)}$ thence increment Y every bit usual.

Cartoon incomplete octants [edit]

The implementations above always depict only complete octants or circles. To draw simply a sure arc from an angle ${\displaystyle \alpha }$ to an angle ${\displaystyle \beta }$ , the algorithm needs first to calculate the ${\displaystyle x}$ and ${\displaystyle y}$ coordinates of these end points, where it is necessary to resort to trigonometric or foursquare root computations (run into Methods of computing square roots). So the Bresenham algorithm is run over the complete octant or circumvolve and sets the pixels simply if they fall into the wanted interval. Afterwards finishing this arc, the algorithm tin be ended prematurely.

If the angles are given as slopes, then no trigonometry or square roots are necessary: simply bank check that ${\displaystyle y/x}$ is between the desired slopes.

Generalizations [edit]

Information technology is also possible to apply the same concept to rasterize a parabola, ellipse, or whatsoever other two-dimensional curve.^[iv]

References [edit]

1. ^ Donald Hearn; Grand. Pauline Baker (1994). Calculator graphics . Prentice-Hall. ISBN978-0-xiii-161530-four.
2. ^ Pitteway, M.L.V., "Algorithm for Drawing Ellipses or Hyperbolae with a Digital Plotter", Reckoner J., 10(three) November 1967, pp 282-289
3. ^ Van Aken, J.R., "An Efficient Ellipse Cartoon Algorithm", CG&A, iv(9), September 1984, pp 24-35
4. ^ Zingl, Alois (Dec 2014). "The Beauty of Bresenham'southward Algorithm: A simple implementation to plot lines, circles, ellipses and Bézier curves". easy.Filter. Alois Zingl. Retrieved sixteen February 2017.

External links [edit]

• Cartoon circles - An article on drawing circles, that derives from a elementary scheme to an efficient one
• Midpoint Circle Algorithm in several programming languages

hopkinsmanclook42.blogspot.com

Source: https://en.wikipedia.org/wiki/Midpoint_circle_algorithm

Share this post